О главной работе М. П. Бронштейна в физике,
или школьникам о квантовой гравитации

В кн. М. П. Бронштейн. Солнечное вещество. Лучи икс. Изобретатели радиотелеграфа. М.: Наука, 1990.

 

 

Геннадий Горелик

В этой книге Матвей Петрович Бронштейн рассказал о замечательных открытиях в физике, химии, астрономии, технике. Но даже внимательно прочитав всю книгу, очень трудно догадаться о собственной специальности ее автора, о тех инструментах и приборах, с помощью которых он сам изучал природу. Трудно поверить, что в научной лаборатории Бронштейна не было ни спектрографов, ни экранов, ни разрядников. Главными его инструментами были ручка и бумага. И, конечно, голова. Эти инструменты служили ему одинаково хорошо при изучении полупроводников и звезд, атомных ядер и Вселенной в целом.

Речь идет, разумеется, о лаборатории теоретической физики. В этой лаборатории даже стол не обязателен. Но зато для успешной работы теоретику надо хорошо понимать, как действуют настоящие физические приборы -- из металла и стекла -- и как с помощью этих приборов делаются открытия. Потому что физика -- наука экспериментальная. Даже теоретическая физика. Матвей Петрович это очень хорошо понимал и поэтому знакомил с физической наукой, рассказывая о замечательных экспериментальных открытиях.

Сам же он в «основное рабочее время» размышлял нередко о вещах, очень далеких от экспериментов. Даже и сейчас, спустя полвека, физика, о которой Бронштейн думал в середине 30-х годов, остается пока недоступной самым изобретательным экспериментаторам. Главное достижение Бронштейна в теоретической физике -- исследование квантовой гравитации -- совпало по времени с его работой над «Солнечным веществом». Читатель, познакомившись по этой книге с экспериментальной физикой, может захотеть узнать и о той физике, которая была профессией автора «Солнечного вещества». Однако для настоящего знакомства с теоретической физикой мало попасть пусть даже и к самому опытному экскурсоводу по Выставке Достижений Научного Хозяйства. Надо еще понимать язык, на котором экскурсовод дает объяснения в павильоне «Теоретическая физика».

Называть приборами, которыми пользуется теоретик, бумагу и ручку -- вообще-то не совсем правильно. Это лишь материал для изготовления приборов. А еще один материал -- и самый главный -- математика. Как выразился великий физик Галилей еще четыре века тому назад, Книга Природы написана на математическом языке. Язык этот особенно нужен в теоретической физике.

Когда у физики экспериментальной -- по разным причинам -- ничего не получается, когда приборы из стекла и металла не в состоянии измерять, вся надежда на приборы, сделанные из математических значков. Не раз уже в истории бывало, что теоретические инструменты, опираясь на предыдущие опыты, приводили к очень странным, прямо-таки неправдоподобным предсказаниям, которые, однако, блестяще оправдывались в новых опытах. К подобным чудесам привыкнуть трудно, но именно они убедили в могуществе теоретической физики и научили доверять таким бесплотным и бесплатным инструментам, как физическая мысль и математический язык.

Чтобы освоить могучий физико-математический язык, надо затратить усилий не меньше, чем на изучение какого-нибудь иностранного языка. А иначе будешь чувствовать себя чужестранцем в стране Физики.

Обходясь школьным запасом физико-математических слов, можно лишь приблизительно понять, о каких трудных физических вопросах размышлял М. П. Бронштейн в 1935 году и почему даже сейчас все еще не удается отвечать на эти вопросы экспериментально.

Среди физических законов, добытых совместными усилиями экспериментаторов и теоретиков, самую простую форму имеют утверждения о постоянстве некоторых физических величин:

a = постоянная.

Вода, откуда бы ее не брать -- из Волги, Миссисипи, из артезианских или даже марсианских источников, всегда имеет одну и ту же плотность -- один грамм в кубическом сантиметре, кипит при 100 градусах и замерзает при нуле.

После того как подобное постоянство перестало удивлять физиков, все такие постоянные были собраны в обширные таблицы. Имеются они и в школьных учебниках. В этих таблицах среди самых разнообразных величин есть три постоянные, с помощью которых легче всего рассказать о главной работе М. П. Бронштейна.

Постоянные эти -- скорость света c, гравитационная постоянная G и постоянная Планка h -- «внешне» ничем особенным не отличаются от других. Однако для теоретика они имеют особое значение.

Первой в физике появилась скорость света c. С нее и начнем.

Очень долго, на протяжении двух столетий после своего измерения, скорость света пребывала в ряду ей подобных: скорость камня, скорость звука, скорость света... Особое уважение она могла заслужить только своим огромным числовым значением: c = 300 000 км/с, или в единицах, принятых у теоретиков,

c = 3 • 10¹⁰ см/с.

Расстояние, которое человек может пройти лишь за целую жизнь, свет проходит за секунду. Недаром так долго скорость света считалась бесконечной.

Только через два с лишним века после первого измерения результаты некоторых опытов со светом заставили посмотреть на величину с новыми глазами. Впрочем, удивиться можно было и до опытов. В самом деле, как можно ответить на вопрос, чему равна скорость камня? Смотря какого камня: лежащего на дороге, брошенного рукой под углом к горизонту или путешествующего в ракете! А скорость света, как показали искусные экспериментаторы, совершенно не зависит от того, лежит ли источник света на дороге или мчится в ракете. Все равно измерения давали одни и те же 300000 км/с. Это очень удивило физиков, -- ничего подобного им до тех пор не встречалось. Сейчас-то легко успокоить тогдашних ученых, обратив их внимание на то, что ни в обыденной жизни, ни в предшествующих физических исследованиях им просто не приходилось иметь дела со скоростями: близкими к огромной величине c.

Представьте себе древнего географа -- обитателя тропической страны, который в своих путешествиях забирается все дальше на север и, наконец, впервые видит и щупает снег. Для этого вещества в его родном языке нет даже названия. А кто поверит в родной жаркой стране его рассказам о твердой холодной воде?!

Так и физики, которым на протяжении столетий вполне хватало ньютоновского языка, не сразу осмелились произнести новое слово науки. А требовалось даже не одно слово, нужно было разработать новый язык, который, во-первых, был бы пригоден для хранения всех накопленных физикой сокровищ, во-вторых, объяснил бы загадку скорости света и, наконец, в-третьих, давал бы возможность предсказывать новое.

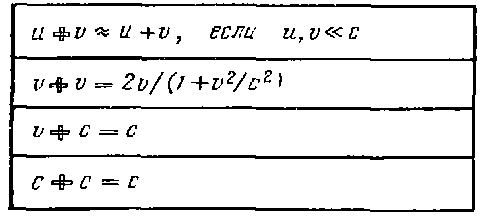
Таблица сложении скоростей в c-теории

Сделать это удалось, только очень сильно изменив язык физики -- изменив представления о пространстве и времени. А ведь любое физическое событие происходит ГДЕ-ТО (в пространстве) и КОГДА-ТО (во времени). Но какое отношение к скорости света имеют общие понятия «ГДЕ» и «КОГДА»? Оказываются, имеют, и не только к скорости света, но и друг к другу. И все потому, что с не просто очень большая скорость, а самая большая. Никакую ракету, никакой сигнал нельзя разогнать до скорости, большей c.

Только учитывая это, можно понять взаимосвязь между ГДЕ и КОГДА. Действительно, предположим, мы хотим узнать, какое из двух событий произошло раньше. Например, какая из двух ламп зажглась раньше, красная или синяя. То есть мы хотим получить ответ на вопрос: «Когда зажглась красная лампа, -- до синей или после?» Если лампы стоят поблизости от наблюдателя и вспышки разделяет порядочный интервал, то в вопросе подвоха не заметно. Если же лампы разнести на многие километры, нетрудно сообразить, что надо как-то учитывать и время, которое потребуется свету на путь от каждой из ламп до наблюдателя. Чтобы сделать лампы равноправными, наблюдателю надо, конечно, расположиться ровно посередине между ними.

Но что же это получается? Чтобы ответить на вопрос КОГДА, нам понадобился ответ на вопрос ГДЕ -- где расположен наблюдатель! В ньютоновские времена можно было надеяться, что используя сигналы, движущиеся гораздо быстрее света (лучше всего -- бесконечно быстро), можно ответить на вопрос КОГДА сам по себе. Но после того как выяснилось, что никакой сигнал не может двигаться быстрее света, такая надежда испарилась.

Оказалось, что по-настоящему точный ответ можно дать только на совместный вопрос ГДЕ-КОГДА, а не на каждый в отдельности. Или, другими словами, пространство, как оказалось, неразрывно связано со временем. Новый физический язык, в котором постоянство скорости света c уже не выглядит загадкой и вопросы ГДЕ-КОГДА не кажутся странными, получил название «Теория относительности». Поскольку в этом языке, в его словаре и грамматике, особо важную роль играет постоянная c, теорию относительности можно назвать c-теорией.

После появления c-теории стало ясно, что постоянная с имеет отношение не только к световым, а ко всем вообще физическим явлениям, поскольку любое событие невозможно описать без понятий пространственных и временных.

А то что в обыденной жизни и в большой части физики присутствие c незаметно, объясняется просто тем, что обыденные скорости ничтожно малы по сравнению со скоростью c. Когда-то ученые люди были уверены, что Земля плоская. Эта уверенность была вполне научной, поскольку опиралась на их реальный жизненный опыт, -- им просто не приходилось иметь дело с расстояниями в тысячи километров (радиус Земли, напомним, -- около шести тысяч километров). А для кого подобные расстояния стали обычным делом, -- путешественники, географы, астрономы -- те и заметили шарообразность Земли, и измерили ее радиус. Точно так же и физики, взявшие в оборот скорости, сравнимые со скоростью света, не могли не заметить ее особые свойства.

В отличие от c гравитационная постоянная G уже при своем появлении имела всемирный характер. Недаром она родилась в законе всемирного тяготения, согласно которому между любыми двумя телами действует сила

F = Gm₁m₂/r²,

где m₁ и m₂ -- массы тел, г расстояние между ними, а постоянная

G = 6, 7 • 10^-8 см³/(с² г).

В течение двух столетий никому из тех, кто знал этот замечательный закон и пользовался им, не приходило в голову, что он верен лишь приближенно.

Кто не решал школьные задачи о движении камня, брошенного под углом к горизонту?! И кто не помнит, что парабола, по которой движется камень, зависит только от его начальной скорости, но не зависит от массы. В электрическом поле движение еще как зависит от электрического заряда, а в гравитационном поле движение от массы, то есть от гравитационного заряда, не зависит! Конечно, если в закон движения (второй закон Ньютона)

m₁a = F

подставить силу F= Gm₁m₂/r², то масса m₁ сократится. Но все равно, не странно ли это? От массы зависит гравитационная сила, которая определяет движение, а само движение от массы не зависит?! Ни форма траектории, ни скорость движения! Прямо не физика, а какая-то геометрия. Там тоже, какие бы линейки не использовать -- из дерева, из натянутой бечевки или света -- свойства фигур и все теоремы остаются одними и теми же.

В геометричности гравитацию заподозрил Эйнштейн. Ему же удалось превратить свои подозрения в замечательную физическую теорию. В эйнштейновской теории гравитации и в самом деле оказалось много геометрии. В этой теории движение масс объясняется не силами, а геометрией искривленного пространства и времени, правильнее сказать -- пространства-времени, потому что постоянная c уже накрепко их связала. Искривленное пространство-время наглядно можно представить себе натянутой упругой пленкой, прогибаемой в некоторых местах грузиками: присутствие вещества искривляет геометрию, а тела всегда движутся по кратчайшим линиям этой геометрии. Чтобы узнать меру искривления, надо массу умножить на коэффициент G/c², чрезвычайно малый из-за малости G и огромности c. Потому-то кривизну пространства-времени так трудно было заметить. Гораздо труднее, чем кривизну земной поверхности.

Учитывая роль постоянных с и G в эйнштейновской теории гравитации, ее с полным правом можно назвать cG-теорией.

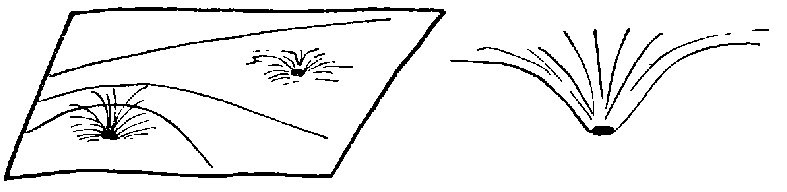
Искривленное пространство-время и вещество в cG-теории

Теперь, наконец, настала очередь самой молодой из интересующих нас трех постоянных. Но родословная у этой самой молодой -- самая древняя. Еще до нашей новой эры греки предположили, что всякое вещество состоит из мельчайших, неделимых частиц -- атомов. Два с лишним тысячелетия атомы были лишь философской гипотезой, которая одним нравилась, другим -- нет. Перевести атомную идею из философии в физику помогла химия. Как нам уже известно по истории солнечного вещества, химики вообще славно потрудились на благо физической науки.

После того как атомное строение вещества стало надежно установленным фактом, физики принялись за сам атом. Не обращая внимания на греческий язык, согласно которому атом неделим, экспериментаторы стали изучать его устройство. Устройство это оказалось на удивление простым, а главное, хорошо знакомым, -- недаром его назвали планетарным. В центре атома, в роли Солнца, -- ядро, а вокруг него движутся, в роли планет, электроны. Только настоящие планеты связаны с Солнцем гравитационной силой, а электроны, как легко догадаться, -- электрической. Однако простота этого сходства оказалась с большим подвохом и даже с двумя.

Один подвох легко понять читателю «Солнечного вещества». Открытию гелия, как читатель, наверное, помнит, очень помогло то обстоятельство, что каждое вещество имеет свой собственный излучательный «отпечаток пальцев» -- спектр. Различие спектров можно было объяснить разницей в числе электронов, содержащихся в атомах разных веществ. Но как понять, что каждый спектр состоит из вполне определенных линий? Откуда в атоме возникает излучение точно определенной частоты, то есть цвета?

Согласно электрической теории электрон, движущийся по окружности, излучает по-разному в зависимости от его скорости и радиуса окружности. Для расчета этого излучения в теории электричества есть специальные формулы, которые прекрасно подтверждаются для самых разнообразных излучателей, начиная от герцевского разрядника и до новейших радио- и телепередатчиков.

Теория электричества может определить, с какой скоростью электрон движется по окружности данного радиуса, а следовательно, и каким будет излучение -- его цвет и яркость. Однако на вопрос, каким может быть радиус орбиты, теория электричества отвечает -- «любым». Стало быть, нет и надежды узнать, какие линии должен излучать данный вид атомов, -- любые! А ведь разноцветные светящиеся картинки, получаемые с помощью призмы в спектроскопе, ясно говорят, что не любые. Натрий -- желтые, калий -- фиолетовые и т. д.

Но планетарное устройство атома, если вдуматься, подстерегала гораздо большая неприятность, даже катастрофа. Ведь согласно электрической теории электрон, вращаясь, непрерывно излучает энергию и при этом все более приближается к ядру, падая на него в конце концов. Этот «конец концов» для атома наступает так быстро, что не успеешь глазом моргнуть. Действительно, разве можно моргнуть за миллиардную долю секунды? Таким образом, если верить ньютоновской механике и теории электричества, атом вообще не может существовать. Значит, верить нельзя. Значит, когда имеешь дело с такими маленькими (по размеру, но не по важности) предметами, надо учитывать какие-то новые физические законы.

И такой новый закон был открыт. В нем отчетливо проявилась штучность, или, как говорят, квантовость, свойственная миру спектральных линий (квант -- отдельная порция). Оказалось, что планетарное устройство атома можно спасти от разрушения, если считать, что электрон имеет право вращаться не по любой орбите с любой скоростью, а только так, что

mvr = nh.

Здесь m и v -- масса и скорость электрона, r -- радиус орбиты, n -- любое целое число: 1, 2, 3,..., а h -- новая физическая постоянная, носящая имя своего открывателя -- Планка. Величина этой постоянной, точнее говоря, ее малость:

h =1,1 • 10^-27 г см²/c

объясняет се незаметность в физике обыденной жизни. Когда соседние орбиты, разрешенные новым законом, отличаются на такую микроскопически малую величину как квант h, это различие заметно, только если сами орбиты микроскопически малы.

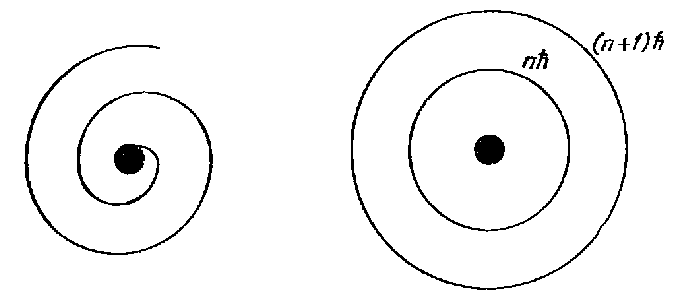
Атом не может существовать без h

Но подлинная теория должна быть максимально точной. Поэтому, когда обнаружилось, что без h ни один атом жить не может, стало ясно, что без учета h в общей теории не обойтись, то есть что нужна cGh-теория, или квантовая теория гравитации.

Первым понял это по-настоящему Матвей Петрович Бронштейн. И в 1935 году, в том же самом году, когда он трудился над историей солнечного вещества, появилось его главное исследование cGh-теории. Построить эту теорию полностью ему не удалось (быть может, просто не успел -- ведь жить ему оставалось два года). Но получил результаты, очень важные для одоления трудной задачи. Что задача эта действительно трудна, можно судить хотя бы по тому, что она и до сих пор, спустя 50 лет, все еще не решена. Физикам еще только предстоит узнать, как можно совместить искривленное непрерывное пространство-время cG-теории с квантовостью h-теории.

Но каким физикам необходима cGh-теория? Какие физические явления без этой теории не понять? Вот, скажем, без c-теории не обойтись при описании движений со скоростью, сравнимой со скоростью света; без cG-теории не обойтись при описании достаточно больших концентраций вещества: когда масса m сосредоточена в области по размеру сравнимой с Gm/c². А когда вступает в действие cGh-теория?

Чтобы ответить на этот вопрос, давайте смастерим подходящий теоретический прибор, из тех, о которых говорилось в начале. Прибор, сделанный не из стекла и металла, а из физических понятий и математических формул.

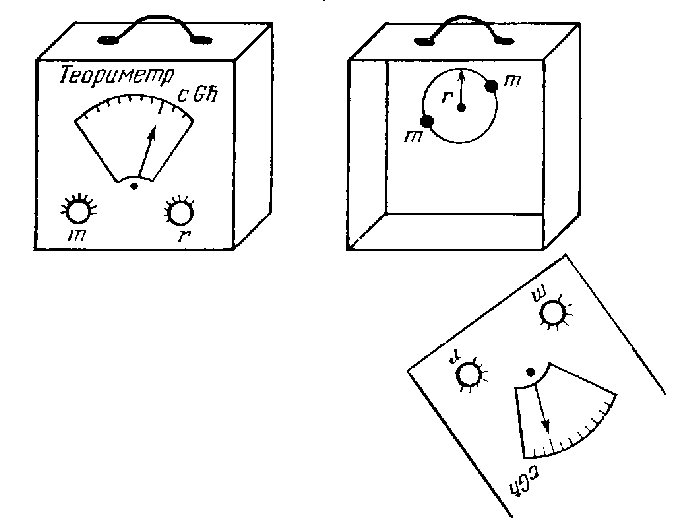
Устройство теориметра

Возьмем две одинаковые точечные массы, запустим их по круговой орбите, на которой пусть их удерживает гравитационная сила взаимного притяжения. Получим нечто вроде гравитационного атома или миниатюрной двойной звезды. Назовем прибор «теориметром», поскольку с его помощью будем измерять состояние теории. Где у нашего прибора ручка регулирования? Их даже две: одна может менять массу m, другая -- радиус орбиты r. Поскольку прибор у нас теоретический, управлять этими величинами можно совершенно произвольно, если, конечно, этому не помешают какие-нибудь законы природы. Подчиним механизм «теориметра» всем физическим законам, выписанным на предыдущих страницах. Ньютоновский закон движения ma = F при подстановке в него центростремительного ускорения a=v²/r и силы тяготения F= Gm²/(2r)² даст

mv²/r=Gm²/(2r)².

Добавим к этому квантовый закон, получим

v² = Gm/4r,

mvr = nh.

Эта система из двух уравнений собственно и есть наш теоретический прибор. По сравнению с «приборами» современной теорфизики, это, конечно, детская игрушка, но ведь и сделали прибор мы из школьной математики.

Когда же стрелка «теориметра» покажет на отметку cGh-физики? Когда скорость v приближается к скорости света с, а целое число n принимает наименьшее значение n = 1. Посмотрим, при каком положении ручек, регулирующих те и г, это достигается. Полагая в уравнениях нашего прибора v = c и n = 1:

c² = Gm/4r,

mcr = h,

легко получить, что cGh-физика наступает при r_cGh = (Gh/c³)^1/2 и m cGh=(hc/G)^1/2 . Подставив значения постоянных c, G и h, получим

r_cGh = 10^-32 см,
m_cGh = 10^-5 г.

Величины эти способны обескуражить. Самое малое расстояние, доступное современной экспериментальной физике, -- 10^-16 см -- во столько же раз больше квантово-гравитационной длины r_cGh, во сколько земной шар больше атома. С учетом такой пропасти, отделяющей эксперимент от r_cGh, говорить что-нибудь определенное о квантово-гравитационной физике может показаться делом совершенно несерьезным. Однако история уже знает похожий случай: теория электричества, созданная в прошлом веке для явлений в масштабе расстояний порядка 1 см, подтверждается в наше время вплоть до расстоянии 10^-16 см. Поэтому теоретики со всей серьезностью видят в cGh-физике (и значит в величине r_cGh) надежду раскрыть устройство элементарных (на сегодняшний день!) частиц, объяснить физический мир в самых малых масштабах.

Что касается квантово-гравитационной массы m_cGh, то она обескураживает своей несуразной величиной -- маленькой, но не очень. Как заметил еще М. П. Бронштейн, это масса самой заурядной пылинки. Правда, чтобы такая пылинка проявила свою квантово-гравитационную суть, ее надо было бы сжать до микроскопических размеров r_cGh.

Однако квантовая гравитация причастна не только к физике микромира. Посмотрим, какая плотность вещества соответствует квантово-гравитационной физике. Полагая, что cGh-масса содержится в cGh-объеме, получим плотность

r_cGh = m_cGh / (r_cGh)³ = 10⁹⁴ г/см³.

Наибольшая плотность, доступная современной экспериментальной физике, плотность в атомном ядре и в центре звезд, меньше квантово-гравитационной плотности в 10⁸⁰ раз. Глядя на это невообразимо большое число, можно подумать, что оно-то уж наверняка не имеет никакого отношения к происходящему в физическом мире. Однако физики, научившись глядеть на наш мир в целом, то есть на Вселенную, поняли, что только учитывая r_cGh, учитывая квантовую гравитацию, можно понять происхождение и устройство Вселенной.

Дело в том, что согласно астрономическим наблюдениям Вселенная расширяется: составляющие ее звездные миры -- галактики -- удаляются друг от друга. Это значит, что вчера галактики были ближе, чем сегодня, а позавчера -- еще ближе. И согласно законам эйнштейновской теории гравитации -- cG-теории, которая управляет расширением Вселенной, в прошлом ее плотность была сколь-угодно большой. А значит, был и такой момент, когда плотность равнялась чудовищной величине r_cGh. Но, как мы уже обнаружили своим «теориметром», для такого состояния вещества власти сG-теории уже не хватает. Становится необходима сGh-теория, или квантовая теория гравитации.

Таким образом, квантовая теория гравитации должна будет объяснить устройство нашего мира и в самых малых и в самых больших масштабах.

Это значение cGh-теории одним из первых увидел Матвей Петрович Бронштейн, написавший еще в 1930 году:

«Будущая физика не удержит того странного и неудовлетворительного деления, которое сделало квантовую теорию «микрофизикой» и подчинило ей атомные явления, а релятивистскую теорию тяготения-«макрофизикой», управляющей не отдельными атомами, а лишь макроскопическими телами. Физика не будет делиться на микроскопическую и космическую: она должна стать и станет единой и нераздельной».