First Steps of Quantum Gravity
and the Planck Values,by Gennady Gorelik
Studies in the history of general relativity. [Einstein Studies. Vol.3].
Eds. Jean Eisenstaedt, A.J. Kox.
Boston: Birkhaeuser, 1992. P.364-379.
1.
The Birth of the Planck Values
2.
Gravitation and
Quanta
3.
Bronstein and His Way
to Quantum Gravity
4. "...
an
essential difference between quantum electrodynamics and
the quantum theory of
the gravitational field." Quantum Limits of General
Relativity
5. The
Planck Values and
Quantum Gravity
6.
Conclusion
Every contemporary discussion of quantum gravity inevitably includes the so-called Planck values, which are combinations of three fundamental constants: c (the velocity of light), G (the gravitational constant), and h (Planck's constant):
x pl = cxGyhz,
where the exponents x, y, z are rational numbers. Depending upon the choice of x, y, z the Planck values can have any dimensionality—length, time, density, and so forth.
Today, the Planck values are connected with the quantum limits of general relativity (GR). Such an interpretation of these values is reached in different ways—from arguments within the framework of tentative variants of quantum-gravitational theory to simple dimensional considerations. Because the latter approach does not require any complex theoretical constructions, one can surmise that the quantum-gravitational role of the Planck values may have been known to Planck himself.
In reality, however, Planck introduced his cGh values
in 1899,
without any connection to quantum gravity. Quantum limits to the
applicability
of general relativity (and, implicitly, their Planck scale) were
first
discovered in 1935 by the Soviet theorist Matvey P. Bronstein
(1906-1938). It
was not until the 1950s that the explicitly
quantum-gravitational significance
of the Planck values was pointed out almost simultaneously by
several
physicists. In the following, the history of the Planck values
will be
reviewed. The topic is an important one, because the Planck
scale is almost the
only element certain to be a part of a future synthesis of
general relativity
and quantum theory (Misner, Thorne, Wheeler 1973).
1. The Birth of the Planck Values
In the fifth installment of his continuing study of irreversible radiation processes (Planck 1899), Max Planck introduced two new universal physical constants, a and b, and calculated their values from experimental data. The following year, he redesignated the constant b by the famous letter h (and in place of a, he introduced k = b/a, the Boltzmann constant).
In 1899, the constant b (that is, h) did not yet have any quantum theoretical significance, having been introduced merely in order to derive Wien's formula for the energy distribution in the black-body spectrum. However, Planck had previously described this constant as universal. During the six years of his efforts to solve the problem of the equilibrium between matter and radiation, he clearly understood the fundamental, universal character of the sought-for spectral distribution.
It was perhaps this universal character of the new constant that stimulated Planck, in that same paper of 1899, to consider a question that was not directly connected with the paper's main theme. The last section of the paper is entitled "Natural Units of Measure" ["Natьrliche Maasseinheiten"]. Planck noted that in all ordinary systems of units, the choice of the basic units is made not from a general point of view "necessary for all places and times," but is determined solely by "the special needs of our terrestrial culture" (Planck 1899, p. 479). Then, basing himself upon the new constant h and also upon c and G, Planck suggested the establishment of
units of length, mass, time, and temperature that would, independently of special bodies and substances, necessarily retain their significance for all times and all cultures, even extraterrestrial and extrahuman ones, and which may therefore be designated as natural units of measure. (Planck 1899, pp. 479-480)
These new units are chosen in such a way that in the new system of units every mentioned constant (c, G, h) is equal to one. Thus, Planck introduced the following units:
lpl = (hG/c3)1/2 = 10-33cm
mpl = (hc/G)1/2 = 10-5g
tpl = (hG/c5)1/2 = 10-43s
(where modern notation and values are used). In cosmology, a "natural unit" of density is also now very popular:
rpl = c5/hG2 = 1094g/cm3.
While this last section of the paper bears only a slight
connection to the
rest, it is strongly connected with Planck's broader philosophy
of physics, in
particular, with his attention to the absolute elements of the
scientific world
picture and his opposition to anthropomorphism in physics
(Goldberg 1976).
Eddington (1918) seems to be the first who attempted to uncover
a theoretical
significance in the Planck length, a significance that may be
the clue to some
essential structure of gravitation. But, both Planck's and
Eddington's
suppositions were ignored or even ridiculed (see, for example,
Bridgman 1922).
The quantum-gravitational meaning of the Planck values could be revealed only after a relativistic theory of gravitation had been developed. As soon as that was done, Einstein pointed out the necessity of unifying the new theory of gravitation with quantum theory. In 1916, having obtained the formula for the intensity of gravitational waves, he remarked:
Because of the intra-atomic movement of electrons, the atom must radiate not only electromagnetic but also gravitational energy, if only in minute amounts. Since, in reality, this cannot be the case in nature, then it appears that the quantum theory must modify not only Maxwell's electrodynamics but also the new theory of gravitation. (Einstein 1916, p. 696).
(For a similar comment, see Einstein 1918.) Einstein obviously had in mind the problem of the instability of the atom. But his conclusion was hardly based on quantitative estimates. Atomic radiation, calculated according to classical electrodynamics, results in the collapse of the atom in a characteristic time interval on the order of 10-10 s (in stark contradiction with reality), whereas atomic gravitational radiation, calculated according to Einstein's formula, is characterized by an enormous time collapse on the order of 1037 s. Thus, there was no reason to worry that the relativistic theory of gravitation would contradict empirical data, but the analogy with electrodynamics determined the direction of Einstein's thinking.
The "cosmological" value of the time of atomic gravitational out-radiation reminds one that during these years Einstein was also thinking about cosmological problems. Even though the effect of gravitational radiation is small, Einstein had to reject its possibility, apparently because of his prerequisites for a cosmology. In a static, eternal universe, any instability of the atom is inadmissible, wholly independently of its magnitude. It is interesting to compare this attitude, quite natural for that time, with the current, more tolerant attitude toward the instability of the proton (Salam 1979). The change is explained by the acceptance of an evolutionary picture of the universe.
For two decades after Einstein pointed out the necessity of a quantum-gravitational theory in 1916, only a few remarks about this subject appeared. There were too many other more pressing theoretical problems (including quantum mechanics, quantum electrodynamics, and nuclear theory). And, the remarks that were made were too superficial, which is to say that they assumed too strong an analogy between gravity and electromagnetism. For example, after discussing a general scheme for field quantization in their famous 1929 paper, Heisenberg and Pauli wrote:
One should mention that a quantization of the gravitational field, which appears to be necessary for physical reasons, may be carried out without any new difficulties by means of a formalism wholly analogous to that applied here. (Heisenberg and Pauli 1929, p. 3)
They grounded the necessity of a quantum theory of gravitation on Einstein's mentioned remark of 1916 and on Oskar Klein's remarks in an article of 1927 in which he pointed out the necessity of a unified description of gravitational and electromagnetic waves, one taking into account Planck's constant h.
Heisenberg and Pauli obviously intended that quantization techniques be applied to the linearized equations of the (weak) gravitational field (obtained by Einstein in 1916). Being clearly approximative, this approach allows one to hope for an analogy with electromagnetism, but it also allows one to disregard some of the distinguishing properties of gravitation—its geometrical essence and its nonlinearity. Just such an approach was employed by Leon Rosenfeld, who considered a system of quantized electromagnetic and weak gravitational fields (Rosenfeld 1930), studying the mutual transformations of light and "gravitational quanta" (a term that he was the first to use).
The first really profound investigation of the quantization of
the
gravitational field was undertaken by Matvey P. Bronstein. The
essential
results of his 1935 dissertation, entitled "The Quantization of
Gravitational Waves," were contained in two papers published in
1936. The
dissertation was mainly devoted to the case of the weak
gravitational field,
where it is possible to ignore the geometrical character of
gravitation, that
is, the curvature of space-time. However, Bronstein's work also
contained an
important analysis revealing the essential difference between
quantum
electrodynamics and a quantum theory of gravity not thus
restricted to weak
fields and "nongeometricness." This analysis demonstrated that
the
ordinary scheme of quantum field theory and the ordinary
concepts of Riemannian
geometry are not sufficient for the formulation of a consistent
theory of
quantum gravity. At the same time, Bronstein's analysis led to
the limits of
quantum-gravitational physics (and to Planck's cGh-values).
3. Bronstein and His Way to Quantum Gravity
In the 1930s, the name of the Leningrad theorist Matvey Petrovich Bronstein (1906-1938) was well known in Soviet physics, and this in spite of Bronstein's youth. He was a friend and colleague of the bright young physicists George Gamow, Lev Landau, and Dmitriy Ivanenko, as well as the astronomers Victor Ambarzumian and Nikolai Kozyrev. Bronstein's papers were published in the main physical journals. In 1932, Dirac's Principles of Quantum Mechanics was published in his translation and with many of his footnotes. At Leningrad University and the Leningrad Physical-Technical Institute, the students and faculty appreciated Bronstein's participation in the journal Physikalische Dummheiten, which circulated in a single copy. Many more readers knew Bronstein's popular scientific articles and books and his three wonderful books for children. The latter are being reprinted today, fifty years after the death of their author. In 1937, Bronstein was arrested and then killed by Stalinism. For two decades, his name was banned as the name of an "enemy of the people."
Bronstein had broad scientific interests—his papers dealt with astrophysics, semiconductors, cosmology, and nuclear physics. But, the investigation of quantized gravity became his most important achievement (see Gorelik 1983; Gorelik and Frenkel 1985, 1990).
One of his first papers of 1926 contained evidence of his acquaintance with general relativity, but the full measure of his knowledge of the topic was in an extensive and profound survey article on relativistic cosmology that he published in 1931. The appearance of this review, which contains sections on the foundations of general relativity, on the formulation of the cosmological problem, and on all of the then-known cosmological models, was stimulated by Hubble's discovery of 1929.
In this article, one finds no doubts about the possibility of constructing a cosmological theory based solely on general relativity. In Bronstein's subsequent papers concerning cosmology, such doubts are characteristic, and they are based on his general conception of physics. Bronstein looked at physics through the "magic cGh cube." He drew a chart describing the structure of theoretical physics based on the role played by the three fundamental constants c, G, and h, and on the corresponding limits of applicability of different theories (ignoring some of these constants). His next paper on the topic (Bronstein 1933b) contains a chapter entitled "Relations of Physical Theories to Each Other and to Cosmological Theory," the basic analysis of which was illustrated by the following scheme:
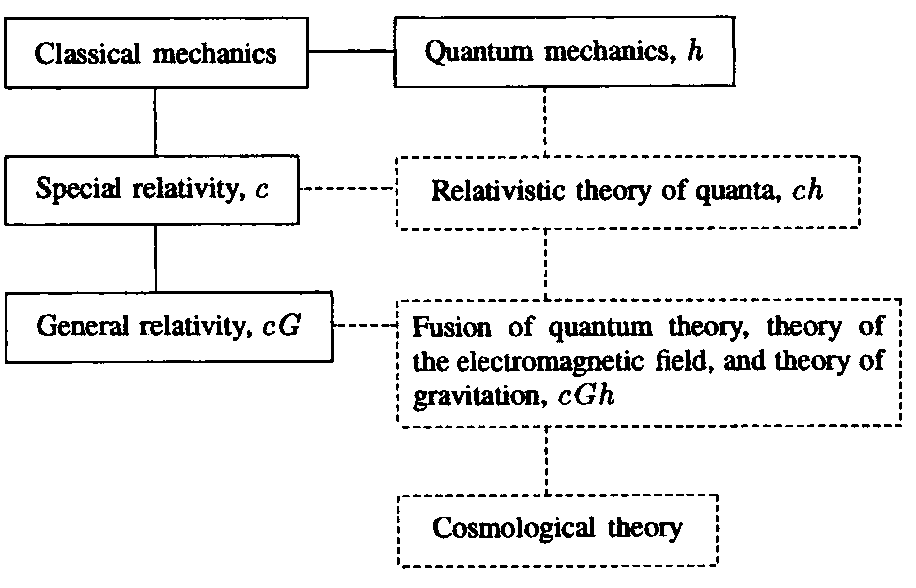
Here, as Bronstein wrote, "solid lines correspond to existing theories, dotted ones to problems not yet solved" (Bronstein 1933b, p. 15). Relativistic quantum theory, that is, ch theory, was then the center of attention. But, as a rule, gravity was ignored.
Bronstein also wrote about the quantum limits of general relativity in other papers, in the context of astrophysics and cosmology (see, for example, Bronstein 1933a). One phrase from Bronstein's popular article of 1929 (which concerned Einstein's attempt to unify gravitation and electromagnetism) reveals his general attitude to the problem of the quantum generalization of general relativity: "The construction of a space-time geometry that could result not only in laws of gravitation and electromagnetism but also in quantum laws is the greatest task ever to confront physics" (Bronstein 1929, p. 25). Thus, it is no surprise that Bronstein chose the quantization of gravitation as the topic of his dissertation (when the system of scientific degrees was introduced in the USSR). However, this choice was rather surprising in the contemporary scientific environment, because in the 1930s, fundamental theorists were concentrating on quantum electrodynamics and nuclear physics.
Bronstein defended his thesis in November 1935. His examiners, the prominent Soviet theorists Vladimir Fock and Igor Tamm, praised the thesis highly as "the first work on the quantization of gravitation resulting in a physical outcome" (Gorelik and Frenkel 1985, p. 317). Bronstein's dissertation and two corresponding publications (Bronstein 1936a, 1936b) were mainly devoted to the quantization of weak gravitational fields, but one of the most important results is an analysis of the compatibility of quantum concepts and classical general relativity in the general case (this latter topic will be examined separately).
Bronstein considered gravitation in the weak-field approximation (where it is described by a tensor field in Minkowski space) in accordance with Heisenberg and Pauli's general scheme of field quantization (Heisenberg and Pauli 1929). From quantized weak gravitation, he deduced two consequences: (1) a quantum formula for the intensity of gravitational radiation coinciding in the classical limit with Einstein's formula, and (2) the Newtonian law of gravitation as a consequence of quantum-gravitational interactions.
One might think that what we see here is merely an expression of the simple requirement of the correspondence principle. In fact, Bronstein's results had real significance, because the peculiar character of the gravitational field (namely, its identification with the space-time metric) gave rise to doubts about the possibility of synthesizing quantum concepts and general relativity. For example, Yakov I. Frenkel (the head of the theoretical department at the Leningrad Physical-Technical Institute, where Bronstein worked) was very sceptical about the possibility of quantizing gravitation, because he, like some other physicists, considered gravitation as a macroscopic, effective property of matter. It should be mentioned that even in the 1960s, Leon Rosenfeld supposed that the quantization of gravitation might be meaningless since the gravitational field probably has only a classical, macroscopic nature (Rosenfeld 1963)—and Rosenfeld was the first to consider a formula for the expression of quantized gravitation. On the other hand, Einstein's attitude was also well known. He believed that the correct full theory was separated from general relativity by a much smaller distance, so to speak, than from quantum theory.
Bronstein's attitude was near the golden mean, since he was
sure that one
should look for the synthesis of both great theories—general
relativity and the
quantum theory. His investigation brought to light deep
connections between the
classical and quantum ways of describing gravitation and so gave
testimony to
the effect that the quantum generalization of general relativity
is both
possible and necessary.
4. "... an essential difference between quantum electrodynamics and the quantum theory of the gravitational field." Quantum Limits of General Relativity
Before obtaining the two mentioned results and just after deducing commutation relations, Bronstein analyzed the measurability of the gravitational field, taking into account quantum restrictions.
The question of measurability had occupied an important place in fundamental physics since Heisenberg had discovered the restrictions on measurability resulting from the indeterminacy relations (restrictions on the measurability of conjugate parameters). As physicists looked toward the development of ch-theory (relativistic quantum theory), the question of measurability attracted great attention, especially after Landau and Peierls rejected in their 1931 paper the concept of an "electromagnetic field at a point," based upon its immeasurability within the ch-framework. This paper led to the detailed and careful analysis of the situation that was undertaken in 1933 by Bohr and Rosenfeld. They saved a local field description in quantum electrodynamics, but at the high price of assuming arbitrarily high densities of mass and electrical charge.
Bronstein had an eye for this subject, and just after Bohr and Rosenfeld's paper, he summed up the situation in a short but clear note (Bronstein 1934). So it was quite natural that in considering quantum gravity Bronstein decided to analyze the problem of the measurability of the gravitational field within the cGh-framework.
He proceeded from the weak-field approximation, where the metric gik = dik + hik , and dikis the Minkowski metric, with hik << 1. In this case, the Einstein field equations have the form
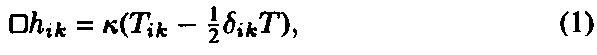
where Tik, is the energy-momentum tensor, and k = 16pG/c2. In order to analyze the measurability of the gravitational field, Bronstein considered the following thought experiment for measuring the value of the Christoffel symbol Гijk (gravitational field strength) by observing the movement of a test body.
In the weak-field approximation, the equation of a geodesic
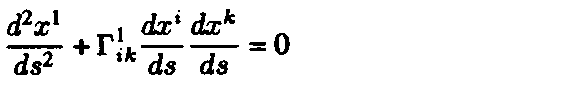
can be written as (x1 = x)
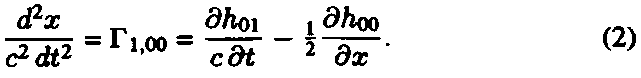
To measure Г1,00 averaged over the volume V and the time interval T, one should measure the component of momentum px of a test body with volume V at the beginning and at the end of the interval T:
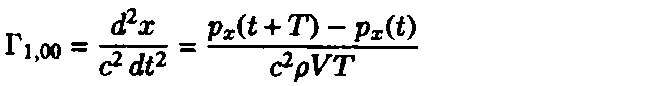
where r is the density of the test body. If the measurement of the momentum has indeterminacy ~Dpx, then
![]()
The indeterminacy Dpx is the sum of two
parts: the ordinary
quantum mechanical term (Dpx)1
= h/Dx, where
Aar is the indeterminacy in the coordinate x, and "the
term
connected with the gravitational field that is created by the
measurer due to
the recoil in the measurement of momentum." The latter term can
be
estimated with help of Eq. (1):
![]()
If a separate measurement of momentum requires a time interval Dt
(<< T), then the indeterminacy in ho\, connected
with the
indeterminacy in the recoil velocity vx ~ Dx/Dt,
is of
the order
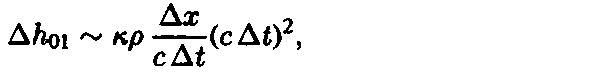
and, in accordance with Eq. (2), DГ1,00
~ krDx. So
the indeterminacy in the momentum that is connected with the
gravitational
field of the test body would be
Two conditions determine the lower bound on the duration At of
the
measurement of momentum. First, it is necessary that Dt >
Dx/c in
order for the recoil velocity to be less than c. Hence,
from Eq. (5), we
get
![]()
Second, from the very meaning of the measurement of the field in
volume V, it
follows that the indeterminacy Dx < V1/3.
Hence,
![]()
Having obtained these two lower limits, Bronstein remarked that
the ratio

"depends on the mass of the test body, being quite
insignificant in the
case of the electron and becoming of order 1 in the case of a
dust particle
weighing one hundredth of a milligram" (Bronstein 1936b,
p. 216).
There are then two limits for DГ, respectively
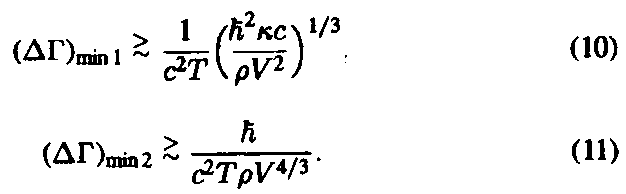
As we have seen, to measure F in a certain volume V as
precisely as possible,
one should use a test body with as large a mass (density) as
possible. Hence,
only the first limit is essential.
Bronstein wrote that the preceding considerations are analogous to those in quantum electrodynamics. But there arises here the essential difference between quantum electrodynamics and quantum gravity, because
in formal quantum electrodynamics, which does not take into consideration the structure of the elementary charge, there is no consideration limiting the increase of density p. With sufficiently high charge density in the test body, the measurement of the electrical field may be arbitrarily precise. In nature, there are probably limits to the density of the electrical charge... but formal quantum electrodynamics does not take these limits into account.... The quantum theory of gravitation represents a quite different case: it has to take into account the fact that the gravitational radius of the test body (krV) must be less than its linear dimensions

(Bronstein 1936b, p. 217)
It follows that Eq. (10) gives "the absolute minimum for the indeterminacy":
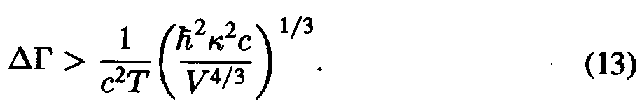
Bronstein understood that "the absolute limit is calculated roughly" (in the weak-field framework), but he believed that "an analogous result will be valid also in a more exact theory." He formulated the fundamental conclusion as follows:
The elimination of the logical inconsistencies connected with this requires a radical reconstruction of the theory, and in particular, the rejection of a Riemannian geometry dealing, as we have seen here, with values unobservable in principle, and perhaps also the rejection of our ordinary concepts of space and time, replacing them by some much deeper and nonevident concepts. Wer's nicht glaubt, bezahlt einen Taler. (Bronstein 1936b, p. 218)
(The same German phrase concludes one of the Grimm brothers' very improbable fairy tales).
In such a way, the quantum limits of general relativity were revealed for the first time. The only thing lacking for the modern theorist is the Planck scale of these limits. Of course the Planck values were implicitly present, because all three constants c, G, and h, were involved in Bronstein's analysis. One such value, the Planck mass (hc/G)1/2, appeared in Bronstein's text, "a dust-particle weighing one hundredth of a milligram."
It is not difficult to supplement Bronstein's reasoning in order to demonstrate the Planck scale of quantum gravity, if only one tries to measure the gravitational field as precisely as possible in a volume as small as possible (Gorelik 1983). Then, one can obtain, for example, the indeterminacy of the metric
Dg = lpl /cT.
The true value of Bronstein's fundamental result concerning the quantum limits of general relativity was not recognized by his contemporaries. For example, Vladimir Fock had, on the whole, a very high opinion of Bronstein's dissertation, but in a summary written for an abstract journal, Fock gave only the following vague characterization of this important result: "a few observations on the measurability of the field quantities are appended" (Fock 1936, p. 88).
In the 1930s, it was much easier to unite the constants c and
h with
e, me, and mp than with G
(Heisenberg
1930). Only a deep understanding of the structure of theoretical
physics
allowed one to single out just the three constants c, G, and
h. It
was clear to Bronstein that a synthesis of general relativity
and quantum
theory would be inevitable for astrophysics, cosmology, and
fundamental physics
in general (Gorelik and Frenkel 1985, 1990). Today, when such a
synthesis is
eagerly sought, Bronstein's analysis of measurability does not
lose its
significance.
5. The Planck Values and Quantum Gravity
For two decades after Bronstein's work, there was calm in the field of quantum gravity. Only in the mid-1950s did the length l0 = (Gh/c3)1/2 appear almost simultaneously in a few different forms in a few papers. For example, in 1954, Landau pointed out that the length l= G1/2h/ce (= a-1/2l0, very near to the Planck length) is the limit of the region outside of which quantum electrodynamics cannot be considered as a self-consistent theory because of the necessity of taking into account gravitational interactions (Gm2/r ~ e2/r, when m ~ p/c ~ h/lc) (Abrikosov, Landau, Khalatnikov 1954).
In a report at the Bern relativity jubilee conference in 1955, Oskar Klein remarked that l0 corresponds to the gravitational limit of the region of applicability of special relativistic quantum theory. He reasoned in the following way. A relativistic particle represented by a wave packet in volume l3 has energy hc/l and mass h/cl. A difference between the gravitational potentials at the center and the edge of the wave packet Df ~ Gh/cl2 would not change the metric significantly if Df << c2 or l>> l0 (Klein 1954, 1956, p. 61). In his discussion of Klein's report, Wolfgang Pauli also referred to Landau's remark and conjectured that there is a connection between the problem of the quantization of gravity and the problem of divergences in quantum field theory (Pauli 1956, p. 69). Such a possibility continues to attract the attention of theorists.
The most famous quantum-gravitational interpretation of the length l0 was developed in John Archibald Wheeler's 1955 paper entitled "Geons." The main subjects of the paper are hypothetical gravitational-electromagnetic pure field configurations (geons). In addition, Wheeler evaluated the manner in which quantum fluctuations of the metric Dgik depend on a characteristic space scale L. Using Feynman quantization, he showed that Dgik ~ l0/L, that is, the fluctuations become significant when L ~ l0. Thus, the length l0 = (Gh/c3)1/2 corresponds to the quantum limits of general relativity. This is the approach that became the most popular.
The term "Planck values," which is now generally accepted, was
introduced later (Misner and Wheeler 1957). According to
Wheeler, he did not
know in 1955 about Planck's "natural units" (private
communication).
A history of the Planck values provides interesting material for reflections on timely and premature discoveries in the history of science. Today, the Planck values are more a part of physics itself than of its history. They are mentioned in connection with the cosmology of the early universe as well as in connection with particle physics. In considering certain problems associated with a unified theory (including the question of the stability of the proton), theorists discovered a characteristic mass ~ 1016mp (mpis the proton mass). To ground such a great value, one first refers to the still greater mass 1019mp. In the words of Steven Weinberg:
This is known as the Planck mass, after Max Planck, who noted in 1900 that some such mass would appear naturally in any attempt to combine his quantum theory with the theory of gravitation. The Planck mass is roughly the energy at which the gravitational force between particles becomes stronger than the electroweak or the strong forces. In order to avoid an inconsistency between quantum mechanics and general relativity, some new features must enter physics at some energy at or below 1019 proton masses. (Weinberg 1981, p. 71).
The fact that Weinberg takes such liberties with history in this quotation is evidence of the need to describe the real historical circumstances in which the Planck mass arose. As we saw, when Planck introduced the mass (ch/G)1/2 (~ 1019mp) in 1899, he did not intend to combine the theory of gravitation with quantum theory; he did not even suppose that his new constant would result in a new physical theory. The first "attempt to combine the quantum theory with the theory of gravitation," which demonstrated that "in order to avoid an inconsistency between quantum mechanics and general relativity, some new features must enter physics," was made by Bronstein in 1935. That the Planck mass may be regarded as a quantum-gravitational scale was pointed out explicitly by Klein and Wheeler twenty years later. At the same time, Landau also noted that the Planck energy (mass) corresponds to an equality of gravitational and electromagnetic interactions.
Theoretical physicists are now confident that the role of the
Planck values
in quantum gravity, cosmology, and elementary particle theory
will emerge from
a unified theory of all fundamental interactions and that the
Planck scales
characterize the region in which the intensities of all
fundamental
interactions become comparable. If these expectations come true,
the present
report might become useful as the historical introduction for
the book that it
is currently impossible to write, The Small-Scale Structure
of Space-Time.
Acknowledgment: The author is thankful to Jean
Eisenstaedt and Don
Howard for their help in preparing this report
Abrikosov, Alexei, Landau, Lev,
and
Khalatnikov, Isaac (1954). "Asimptoticheskoe vyrazhenie dlya
fotonnoy
funktsii Grina v kvantovoy elektrodinamike." ["Asymptotic
Expression
for the Green's Function of a Photon in Quantum
Electrodynamics."] Doklady
Akademii Nauk
SSSR 95:
1177-1180.
Bohr,
Niels, and
Rosenfeld, Leon (1933). "Zur Frage der Messbarkeit der
elektromagnetischen
Feldgrцssen."
Det Kongelige
Danske Videnskabernes Selskab. Mathematisk-Fysiske
Meddelelser 12 (No. 8):
3-65.
Bridgman, Percy W. (1922). Dimensional Analysis. New Haven, Connecticut: Yale Univ. Press.
Bronstein, Matvey Petrovich (1929). "Vsemirnoe tyagotenie i elektrichestvo (novaya teoriya Eynshteyna)." ["Universal Gravity and Electricity (New Einstein Theory)."] Chelovek i priroda 8: 20-25.
——— (1931). "Sovremennoe sostoyanie relyativistskoy kosmologii." ["The Modern State of Relativistic Cosmology."] Uspekhi Fizicheskikh Nauk 11: 124-184.
——— (1933a). "Vnutrennee stroenie zvezd i istochniki zvezdnoy energii." ["Inner Structure of Stars and Sources of Stellar Energy."] Uspekhi Astro-nomicheskikh Nauk. Sbomik 2: 84-103.
——— (1933b). "K Voprosy o vozmozhnoy teorii mira kak tselogo." ["On the Question of a Possible Theory of the World as a Whole."] Uspekhi As-tronomicheskikh Nauk. Sbomik 3: 3-30.
——— (1934). "K Voprosy o
relyativistskom
obobshchenii printsipa neopredelen-nosti." ["On the Question
of a
Relativistic Generalization of the Indeterminacy Principle."]
Doklady Akademii Nauk
SSSR 1:
388-390.
——— (1936b). "Kvantovanie gravitatsionnykh voln." ["Quantization of Gravitational Waves."] Zhurnal Eksperimentalnoy i Teoreticheskoy Fiziki 6: 195-236.
Eddington, Arthur (1918). Report
on the
Relativity Theory of Gravitation. London: Fleetway Press.
Einstein,
Albert
(1916). "Nдherungsweise
Integration der
Feldgleichungen der Gravitation." Kцniglich Preussische Akademie
der Wissenschaften (Berlin).
Sitzungsberichte:
688-696.
———
(1918).
"Ьber
Gravitationswellen." Kцniglich Preussiche Akademie der
Wissenschaften (Berlin). Sitzungsberichte:
154-167.
Fock,
Vladimir
(1936). Abstracts of Bronstein 1936a, 1936b. Zentralblatt
fьr Mathematik und ihre
Grenzgebiete 14:
87-88.
Goldberg, Stanley (1976). "Max Planck's Philosophy of Nature and His Elaboration of the Special Theory of Relativity." Historical Studies in the Physical Sciences 7: 125-160
Gorelik, Gennady (1983). Razmernost prostranstva: istoriko-metodologicheskiy analiz. [Dimensionality of Space: Historical and Methodological Analysis.] Ch. 5, "Kvantovye granitsy klassicheskoy geomtrii OTO." ["Quantum Limits of Classical Geometry of General Relativity."] Moscow: University Press.
Gorelik, Gennady, and Frenkel, Victor Ja. (1985). "M. P. Bronstein i kvantovaya teoriya gravitatsii." ["M. P. Bronstein and the Quantum Theory of Gravitation."] In Eynshteynovskiy Sbomik 1980-1981. Moscow: Nauka, pp. 291-327.
——— (1990). Matvey Petrovich Bronstein (1906-1938). Moscow: Nauka.
[——— (1994) [Matvei
Petrovich
Bronstein and Soviet Theoretical Physics in the Thirties. Basel-Boston:
Birkhaeuser]
Heisenberg,
Werner
(1930). Die physikalischen Prinzipien der Quantentheorie.
Stuttgart:
S. Hirzel.
Heisenberg,
Werner,
and Pauli, Wolfgang (1929). "Zur Quantendynamik der
Wellenfelder." Zeitschrift fьr
Physik 56:
1-61.
Klein,
Oskar
(1927). "Zur fьnfdimensionalen
Darstellung der
Relativitдtstheorie."
Zeitschrift fьr Physik 46: 188-208.
——— (1954). "Aktuella Problem Kring Fysikens Sma och Stora Tal." Kosmos (Sweden) 32: 33.
——— (1956). "Generalization of Einstein's Theory of Gravitation Considered from the Point of View of Quantum Field Theory." In Mercier and Ker-vaire, eds. 1956, pp. 58-68.
Landau, Lev (1955). "On the Quantum Theory of Fields." In Niels Bohr and the Development of Physics. Wolfgang Pauli, Leon Rosenfeld, and Victor Weisskopf, eds., Oxford: Pergamon, pp. 52-69.
Landau, Lev, and Peierls, Rudolf
(1931). "Erweiterung
des
Unbestimmtheitsprinzips fьr die
relativistische
Quantentheorie." Zeitschrift fьr Physik 69: 56-69.
Mercier, Andre, and Kervaire, Michel, eds. (1956). Fьnfzig Jahre Relativitдtstheorie. Bern, 11-16 Juli 1955. (Helvetica Physica Acta. Supplementum 4.) Basel: Birkhaьser.
Misner, Charles, and Wheeler, John Archibald (1957). "Classical Physics as Geometry: Gravitation, Electromagnetism, Unquantized Charge, and Mass as Properties of Curved Empty Space." Annals of Physics 2: 525-603.
Misner, Charles, W., Thorne, Kip S., and Wheeler, John Archibald (1973). Gravitation. San Francisco: Freeman.
Pauli, Wolfgang (1956). Discussion following Klein 1956. In: Mercier and Ker-vaire, eds., 1956, pp. 68-69.
Planck,
Max
(1899). "Ьber
irreversible Strahlungsvorgдnge. Fьnfte
Mitteilung." Kцniglich Preussische Akademie
der Wissenschaften (Berlin). Sitzungsberichte:
440-480.
Rosenfeld, L6on (1930). "Ьber die Gravitationswirkungen des Lichtes." Zeitschrift fьr Physik 65: 589-599.
——— (1963). "On Quantization of Fields." Nuclear Physics 40: 353-356.
Salam, Abdus (1979). "Gauge Unification of Fundamental Forces. The 1979 Nobel Prize Address." Reviews of Modem Physics 52 (1980): 525-538.
Weinberg, Steven (1981). "The Decay of the Proton." Scientific American 244 (June): 64-75.
Wheeler, John Archbald (1955). "Geons." Physical Review 97: 511-536.